All Pairs Shortest Path Negative Weights
If we can do that transformation and this is not negative then. For k 1 to n do new dm 1 ik w.
All Pairs Shortest Paths Ppt Download
In computer science the FloydWarshall algorithm is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights.

. Thats the goal for today. If some path from s to v contains a negative cost cycle there does not exist a shortest s-v path. It is guaranteed that G has no negative cycles.
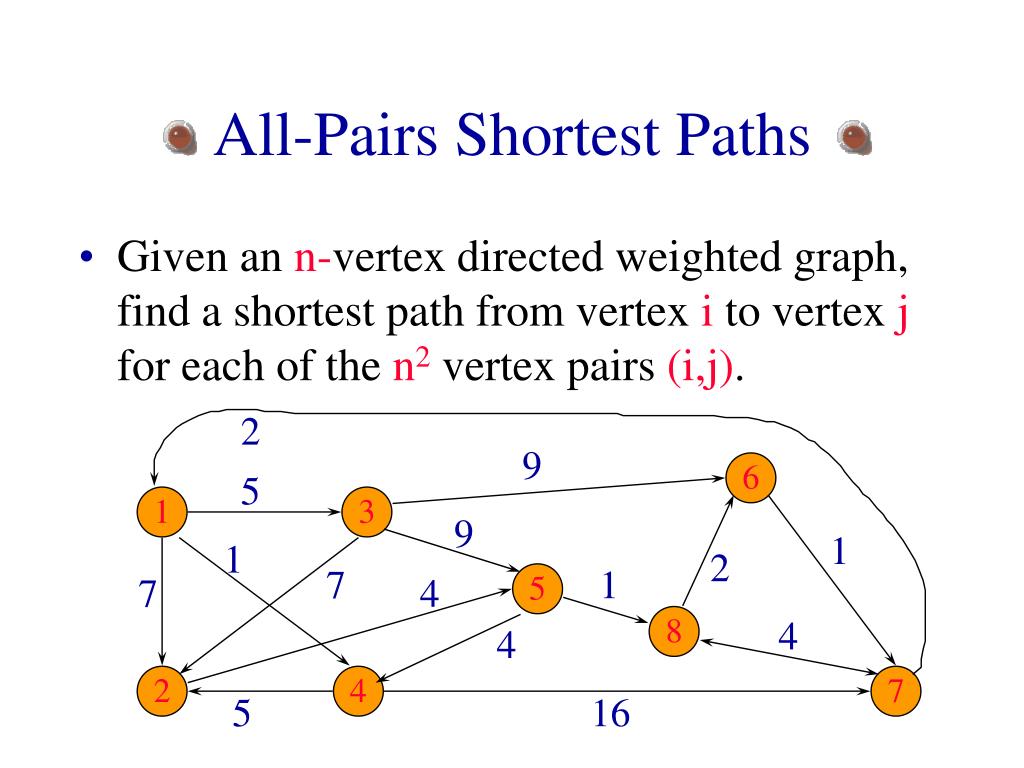
Given all pairs shortest paths matrix find graph with minimum total sum of. Given a directed weighted graph. The problem to make a distances table between all pairs of cities in a Roads Atlas.
Let P be such a. We are still using the raw L14 slides pdf Here are the annotated slides from Mar 21 and annotated slides from Mar 22. A single execution of the algorithm will find the lengths of shortest paths between all pairs of vertices.
Otherwise there exists one that is simple. The shortest path SP from node s. We have discussed Floyd Warshall Algorithm for this problem.
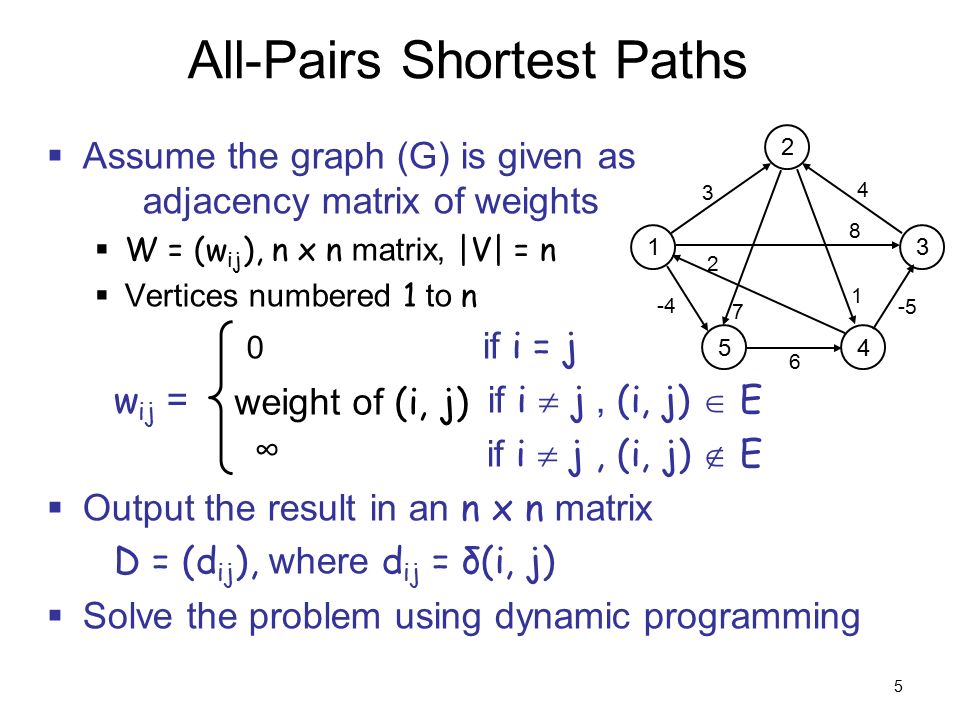
Chapter 25 of Introduction to Algorithms 3rd Edition Thomas H. The problem is to find shortest paths between every pair of vertices in a given weighted directed Graph and weights may be negative. Find the shortest paths between all pairs of vertices in a graph.
Now assume that Cij are not constant but rather can take two values Aij and Bij where 0. A shortest path under each weight function is a shortest path under the other weight function For all u v E ŵu v 0. Shortest paths in graphs with negative edge weights.
Here we assume that there are no cycles with zero or negative cost. And then a -nine makes it one. All-Pairs Shortest Paths II Supplemental reading in CLRS.
But the actual shortest path goes over to four and then over to one and down to two for a weight of ten. Same combinatorial structure just different edge weights. The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs where the vertices correspond to intersections.
Find all the special graphs which can reduced to the shortest paths graph. 12 2013 Based in part on Section 68 1. Let w be a function that maps each edge in E to an integer which can be positive 0 or negative.
For all u v V p is a shortest path from u to v using w iff p is a shortest path from u to v using ŵ. Although it does not return details of the paths themselves it is possible to reconstruct the paths with simple. The All-Pairs Shortest Paths Problem Given a weighted digraph with weight function is the set of real numbers determine the length of the shortest path ie dis-tance between all pairs of vertices in.
The tabular output of the all-pairs shortest-paths algorithms presented in this chapter is an n n matrix D d ij where entry d ij contains the weight of a shortest path from vertex i to vertex j. All-Pairs Shortest Paths Floyd Warshall Algorithm. That is if we let ij denote the shortest-path weight from vertex i to vertex j as in Chapter 25 then dij ij at termination.
Here you can easily use Floyd-Warshall or use Dijkstra n times or whatever and then just to find the maximum among all n2 shortest paths. A b d c e 20 12 5 4 17 3 8 3 20 5 10 4 4 4 a b d c e. S v W cW 0 3 5 4-6 7-4 4 Shortest Paths with Negative Weights OPTi v length of shortest s-v path using at most i arcs.
All weights are non-negative. Version of October 28 2016 All-Pairs Shortest Paths 12 26. Where is the shortest distance from node.
So theres a way to get from zero to three with a weight path weight just one. When the graph is dense. Dijkstra for negative weights by adding a constant.
Using Johnsons algorithm we can find all pair shortest paths in O V2log V VE time. Because of the -nine. Shortest Path Problem Shortest Path with Negative WeightsGiven directed graph G with weighted edges duv that may be positive or negative nd the shortest path from s to t.
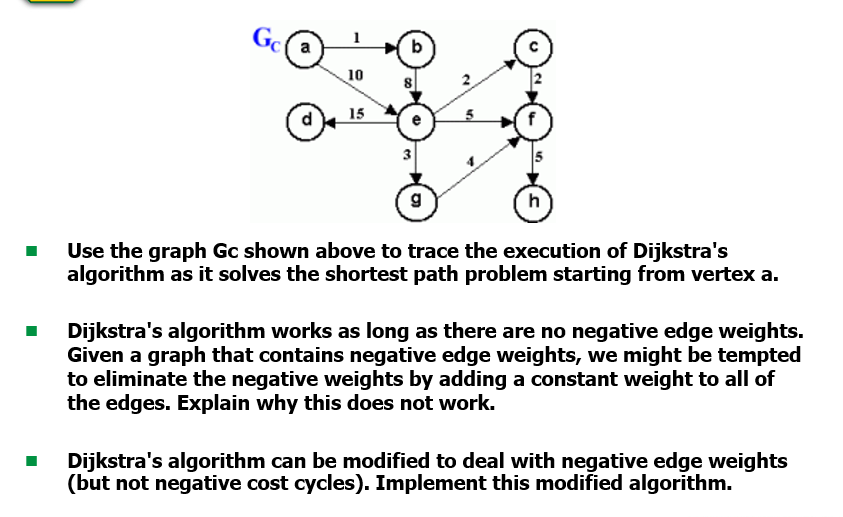
For m 1 to n 1 do for i 1 to n do for j 1 to n do min 1. In graph theory the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized. Correctness of Dijkstras algorithm.
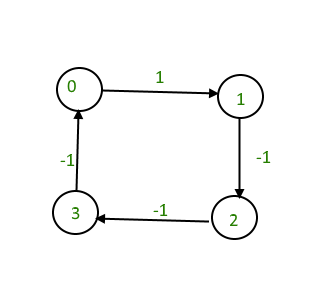
Shortest Paths with Negative Weights Slides by Carl Kingsford Feb. With Johnsons algorithm we can solve the all-pairs shortest-paths problem in networks that contain no negative cycles in time proportional to V E log d V where d 2 if E 2 V and d EV otherwise. Shortest Paths with Negative Weights Negative cost cycle.
We have 2 sets of vertices at any step of the algorithm. Running time On4 much worse than the solution using Dijkstras algorithm. Shortest paths with negative weights Materials.
Show how to modify the all-pairs shortest path algorithm so that it detects negative-weight cycles A negative-weight cycle is a cycle whose total length is negative. And we want shortest paths-- we want these weights to all be non-negative. Floyd Warshalls all pairs shortest paths algorithm works for graphs with negative edge weights because the correctness of the algorithm does not depend on edges weight being non-negative while the correctness of Dijkstras algorithm is based on this fact.
See Properties 2122 through 2124 and the summary in the previous paragraph. Then the running time will be. Recall that if all edge weights are nonnegative then repeated application of Dijkstras algorithm using a Fibonacci heap gives the all-pairs shortest paths in V2lgV VE time.
Suppose you have to find the maximal shortest path between any two nodes i and j. Output a matrix. All Pairs shortest paths.
And we want shortest paths if theres a shortest path in G it continues to be a shortest path in the reweighted graph. Let G VE be a directed graph. Normalizing edge weights and the effect on Dijkstras algorithm.
All-Pairs Shortest Paths APSP Input. If the edge weights can be negative run the Bellman-Ford algorithm. The worst-case bound on the running time is immediate from Properties.
Rivest and Clifford Stein. If new min then min new end end dm ij min. Time complexity of Floyd Warshall Algorithm is Θ V 3.
Section 253 71 Johnsons Algorithm The FloydWarshall algorithm runs in V3 time. If the graph contains a. Saying the shortest way to get from zero to three is is Is to take this edge of three which has weight two.
Given a set of vertices V in a weighted graph where its edge weights w u v can be negative find the shortest path weights d s v from every source s for all vertices v present in the graph. Problem of Finding All Pairs of Shortest Path.
In Java For The Graphs In Your Lecture Slides Verify Chegg Com
Ppt All Pairs Shortest Paths Powerpoint Presentation Free Download Id 472097

All Pairs Shortest Path Algorithm Example Dynamic Design Algorithms Lec 46 Bhanu Priya Youtube

Bellman Ford Algorithm Simple Implementation Geeksforgeeks
Ics 311 19 All Pairs Shortest Paths

Algorithms All Pairs Shortest Path Ppt Video Online Download
Detecting Negative Cycle Using Floyd Warshall Geeksforgeeks

All Pairs Shortest Paths Floyd Warshall Algorithm Techie Delight
Ics 311 19 All Pairs Shortest Paths

Single Source Shortest Paths Bellman Ford Algorithm Techie Delight
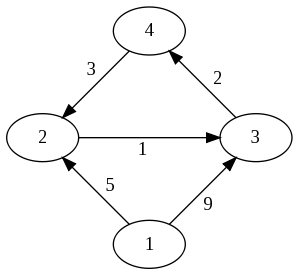
Cs140 All Pairs Shortest Paths

Single Source Shortest Paths Dijkstra S Algorithm Techie Delight

Johnson S Algorithm For All Pairs Shortest Paths Implementation Geeksforgeeks
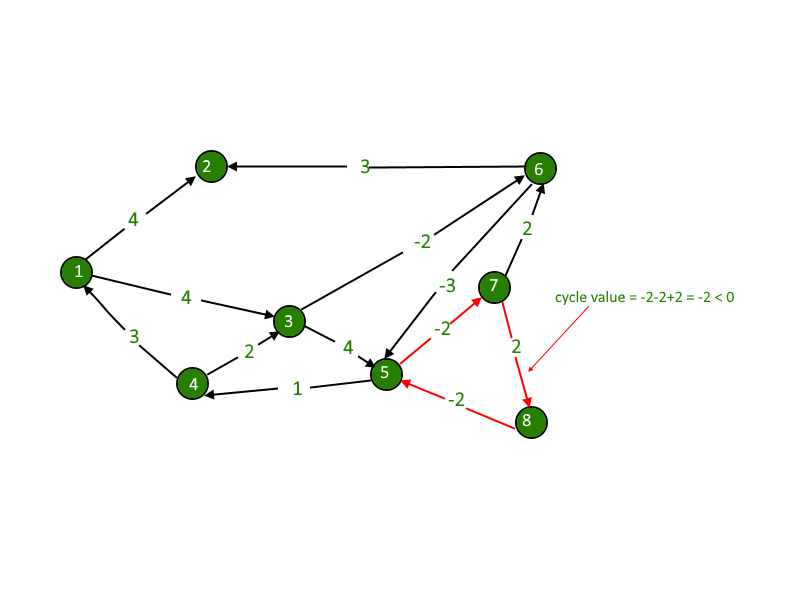
Detecting Negative Cycle Using Floyd Warshall Geeksforgeeks

Johnson S Algorithm For All Pairs Shortest Paths Implementation Geeksforgeeks

All Pairs Shortest Paths Shortest Paths Graph Algorithms Informit

Johnson S Algorithm For All Pairs Shortest Paths Implementation Geeksforgeeks
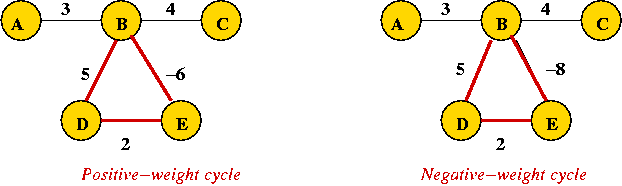
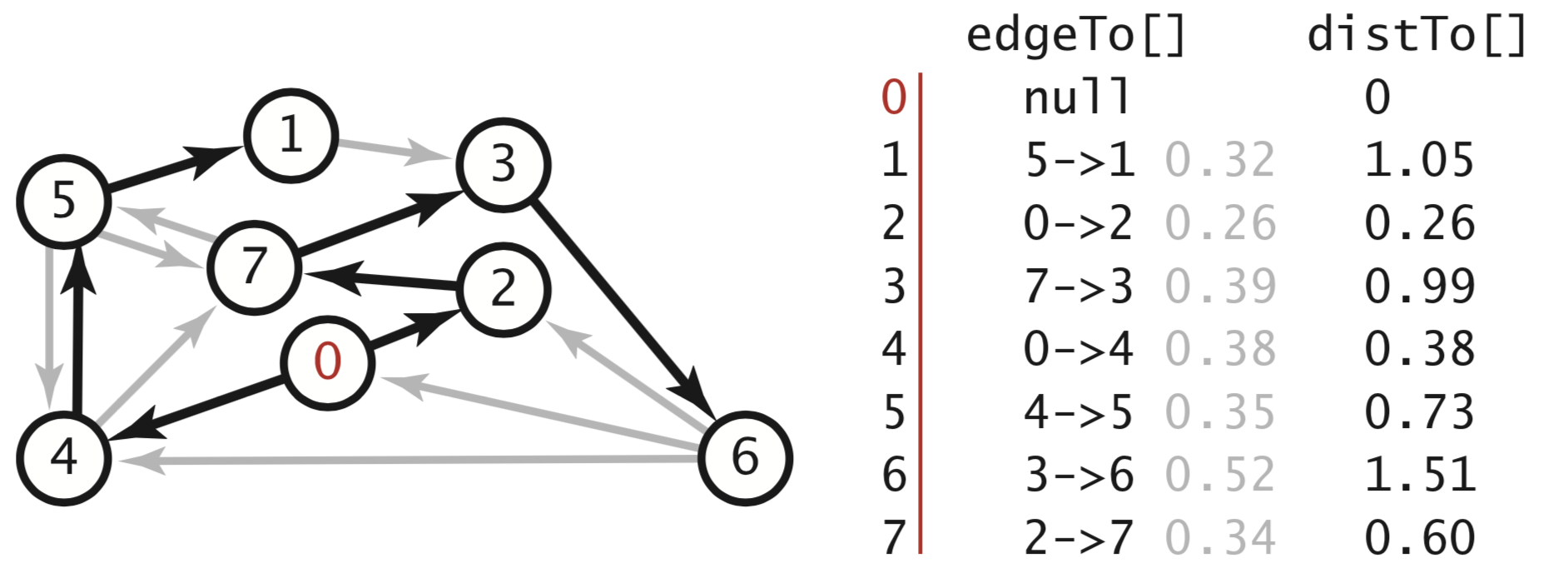
Comments
Post a Comment